[백준] 9663 C++ N-Queen (백트랙킹)

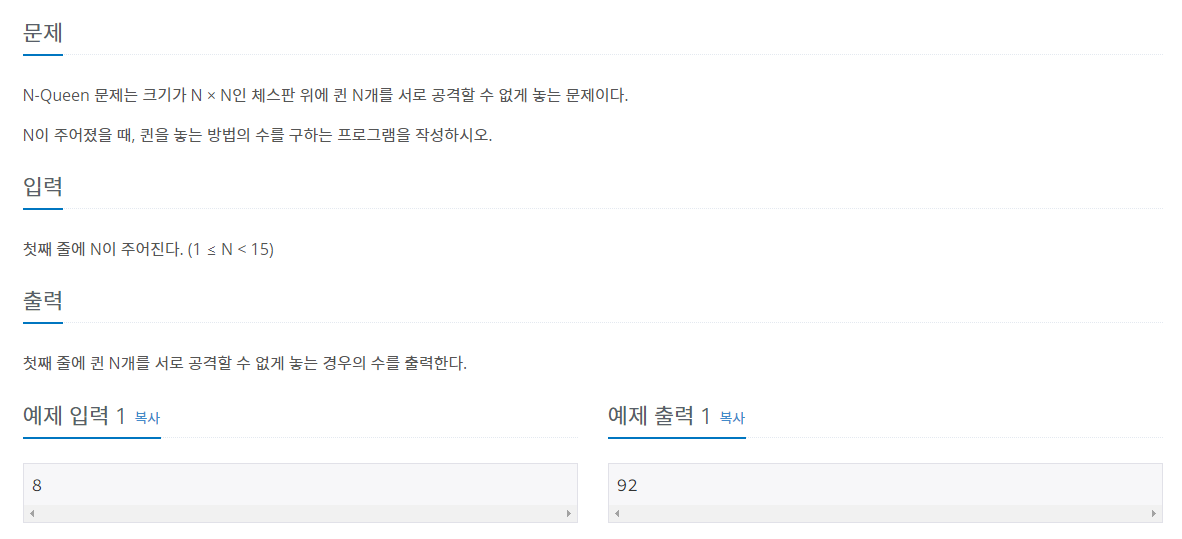
- 문제 설명

 

- 문제 풀이

백트랙킹의 가장 대표적인 문제 N-Queen이다. 기본적인 체스 룰을 알면 규칙은 쉽게 알 수 있다.

체스말 퀸은 같은 행, 열에는 위치할 수 없으므로 N*N 크기의 배열을 만들필요 없이 크키가 N인 일차원 배열을 만든 후 각 열에 몇번째 행에 퀸이 있는지 저장만 하면 된다.

 

한 행씩 퀸을 배치해가며 check 함수를 통해 배치한 퀸과 그 전에 배치했던 퀸들이 겹치지 않는다면 depth를 늘려간다.

depth가 크기 N만큼 늘어났다면, 겹치지 않는 퀸의 경우의 수가 되었단 것이므로 경우의 수를 하나 늘려준다.

 

예를 들어, N = 4라면 아래와 같은 배치의 경우의 수 두 가지가 나온다.

 

같은 행과 열에 있는지에 대해서 체크하는건 간단하지만, 대각선에 대해서는 곧바로 생각해 내긴 힘들다.

다음과 같은 수식으로 같은 대각선에 존재하는 좌표인지 체크할 수 있다.

예를 들어 기존에 있던 퀸의 좌표를 (X, Y)라 하고 새로 배치한 좌표를 (A, B)라고 하면 X-A = Y-B를 만족한다.

코드에서 abs(col[depth] - col[i]) == depth - i 로 표현했는데, depth는 무조건 i보다 크지만 col[depth]는 col[i]보다 크기도 하고 작기도 하므로 절댓값을 씌워준다.

 

- 코드

#include <iostream>
#define MAX 15
using namespace std;

int col[MAX];
int n, cnt = 0;

bool check(int depth)
{
    for (int i = 0; i < depth; i++)
        if (col[i] == col[depth] || abs(col[depth] - col[i]) == depth - i) // 대각선이거나 같은 라인
            return false;
    // col[i] 가 의미하는 것이 x좌표, i가 의미하는것이 y좌표이므로 차이가 일정하다면 대각선에 있다
    return true;
}

void nqueen(int depth)
{
    if (depth == n)
        cnt++;
    else
    {
        for (int i = 0; i < n; i++)
        {
            col[depth] = i; // 해당 위치에 퀸 배치
            if (check(depth)) // 유효하다면 다음 행 퀸 배치, 유효하지 않다면 현재 행 퀸 배치 변경
                nqueen(depth + 1);
        }
    }
}

int main()
{
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);

    cin >> n;

    nqueen(0);
    cout << cnt;

    return 0;
}